電池材料の「協奏的なイオン輸送」を可視化する新理論を開発

2025年12月17日公開

渋滞学がイオンの集団運動を読み解き、高速イオン伝導の物理を解明

プレスリリース研究化学数理・計算科学

ポイント

渋滞学や流体力学の流れ場の解析を応用し、電池材料内部で起こる「協奏的なイオン輸送」という集団運動を、世界で初めて可視化・解析することに成功。
可視化された集団運動とイオン伝導度を1対1で結びつける新しい理論式を発見し、“何個のイオンがどのように連動して動くと伝導度が上がるのか”という電池性能の根本原理を解明。
電池材料の基盤となる新しい物理化学を確立し、イオンの集団輸送を制御する次世代固体電解質の設計指針として期待される成果。

二次元超イオン伝導体Na₂Ni₂TeO₆中の協奏的な輸送が有向グラフ解析により可視化される様子および計算されるイオン伝導度

概要

東京科学大学総合研究院化学生命科学研究所の安藤康伸准教授、東京大学大学院工学系研究科の佐藤龍平助教、澁田靖教授、東北大学材料科学高等研究所（WPI-AIMR）のサウ・カーティック特任講師らの研究グループは、流体力学の流れ場の考え方を応用し、電池材料におけるイオンの集団輸送を可視化する新しい解析手法を開発しました。

研究グループは固体電解質^[用語1]の分子動力学シミュレーション^[用語2]を実施し、シミュレーション中で実際に起こるイオンの協奏的な輸送^[用語3]を、イオンの変位ベクトル同士をつないで構築する「有向グラフ解析^[用語4]」により可視化することに成功しました。さらに、このグラフからイオン伝導度を計算したところ、厳密な統計力学に基づくイオン伝導度の計算式の結果と一致することを確認しました。これにより、固体電解質中で「いくつのイオンが連動して動いているか」という描像を直接得るとともに、集団運動とイオン伝導度を1対1で結びつける新しい理論式を確立しました。本成果は、協奏的な運動を制御して電池性能を高めるための物理化学的基盤を提供するものであり、次世代の固体電解質設計に役立つことが期待されます。

本研究成果は2025年12月12日（米国東部時間）に「Chemistry of Materials」に掲載されました。

発表内容

スマートフォンに使われるリチウムイオン電池をはじめ、電池は現代社会を支える基盤技術です。なかでも全固体型電池^[用語5]は、安全性の向上と高いエネルギー密度の両立が期待される次世代電池として注目されています。しかし、電池の充放電に欠かせないリチウムなどのイオンは、固体内部では液体中に比べて動きにくく、これが性能向上の大きな障壁となっていました。

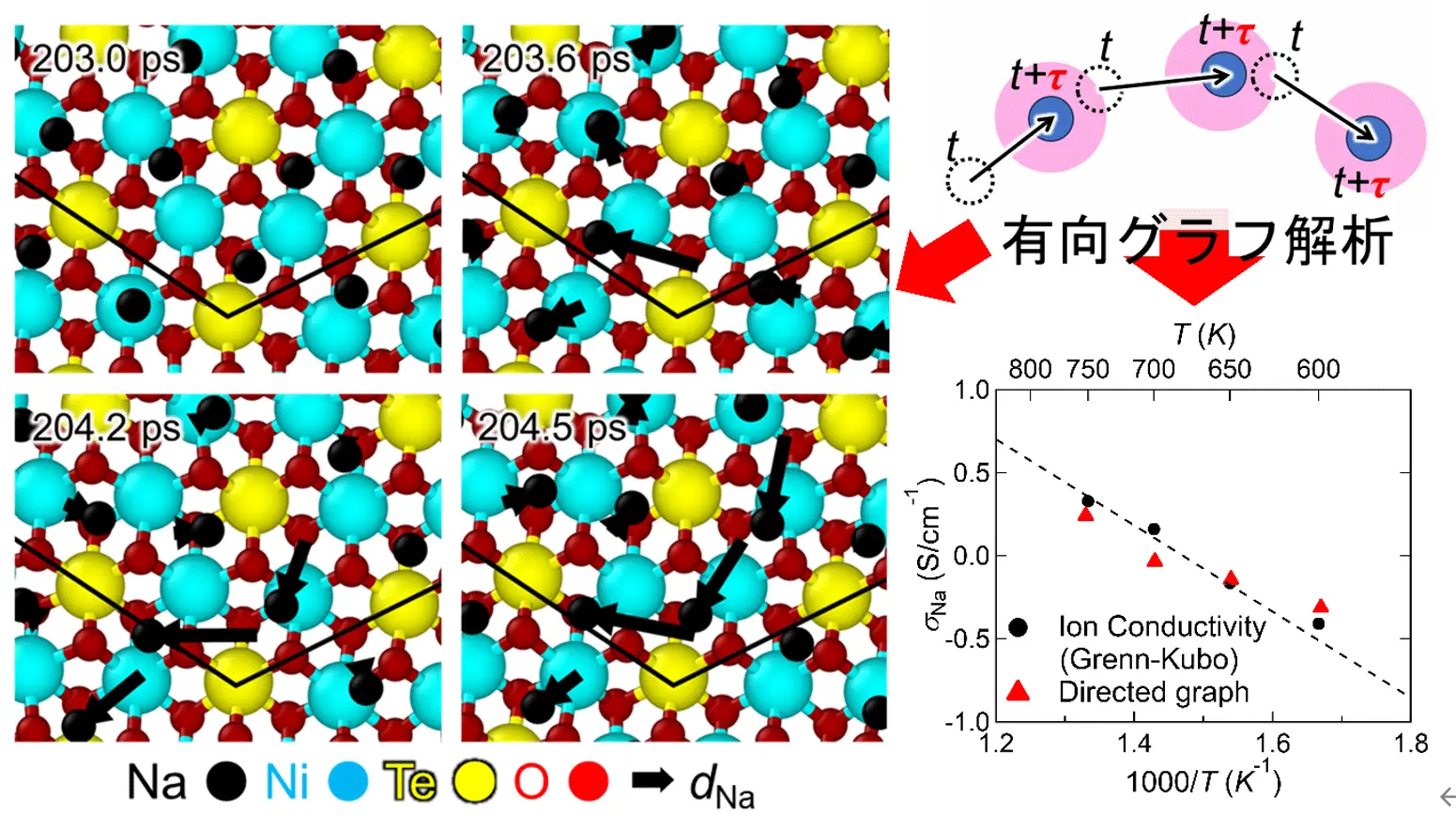
これまで多くの固体電解質材料が開発されてきましたが、その中で特にイオンが速く動く優れた材料には共通点があります。それは、1つのイオンの動きが周囲のイオンを次々に押し出すように誘発し、玉突きのように連鎖的な移動が起こる「協奏的な輸送」（図1）が生じていることです。こうした集団的な動きが起こると、多数のイオンが効率よく輸送に関与できるだけでなく、移動に必要なエネルギーも小さくなるため、電池材料の性能に直結する重要な現象です。

しかし、この協奏的輸送の実態を明らかにすることは簡単ではありません。複数のイオンが互いに影響し合い、さらに周囲の結晶環境とも相互作用するため、問題は三体以上が絡む非常に複雑なものになります。数学的にも、ポアンカレが示したように三体以上の問題は解析解を得ることが極めて難しく、これまでこの現象の具体的な描像やメカニズムは分かっていませんでした。

本研究グループは、自動車に関する渋滞学や流体工学で利用される流れの解析手法を材料に適用し、イオンの輸送を流体として解析することで協奏的な輸送のモデル化に成功しました。

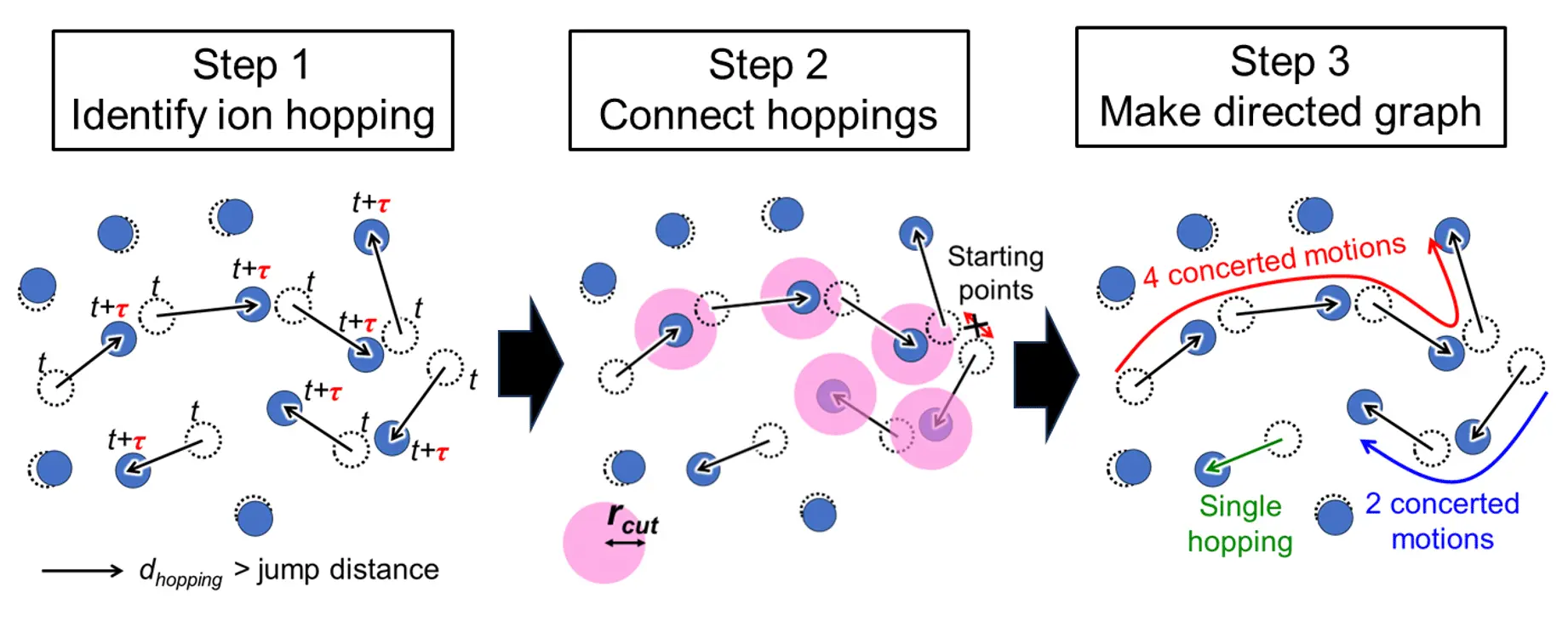
分子動力学シミュレーションでは、イオンの運動方程式を数値的に解くことで、固体中のイオンがどのように動くかを再現します。本研究では、このシミュレーション結果を「イオンが元の安定位置から別の位置へ1回跳ぶかどうか」という短い時間（τ）に区切って解析しました。この短時間では、跳んだイオンの動きは矢印（変位ベクトル）として明確に表すことができます。次に、各変位ベクトル同士が「時間的にも空間的にも近い」場合を、相関のある一連の運動として扱います。空間的な“近さ”は、van Hove 相関関数^[用語6]に基づいて定めた相関距離 r_cut を用いて判断します。具体的には、あるイオンが跳んだ終点と、別のイオンが跳び始める起点が r_cut 以内にある場合、その2つの跳躍は互いに関連した出来事とみなし、変位ベクトル同士をつないでいきます。このようにして得られた変位ベクトルの連結は、有向グラフとして表現され、イオンが“玉突き”のように連動して動く協奏的輸送の経路を可視化します。さらに、この協奏的経路上で「どのイオンが動いたか」にはこだわらず、あたかも1つのイオンが τ の間にどれだけ距離を稼いだかを算出することで、見かけの拡散係数を定義し、イオン伝導度の計算へと結びつけています。

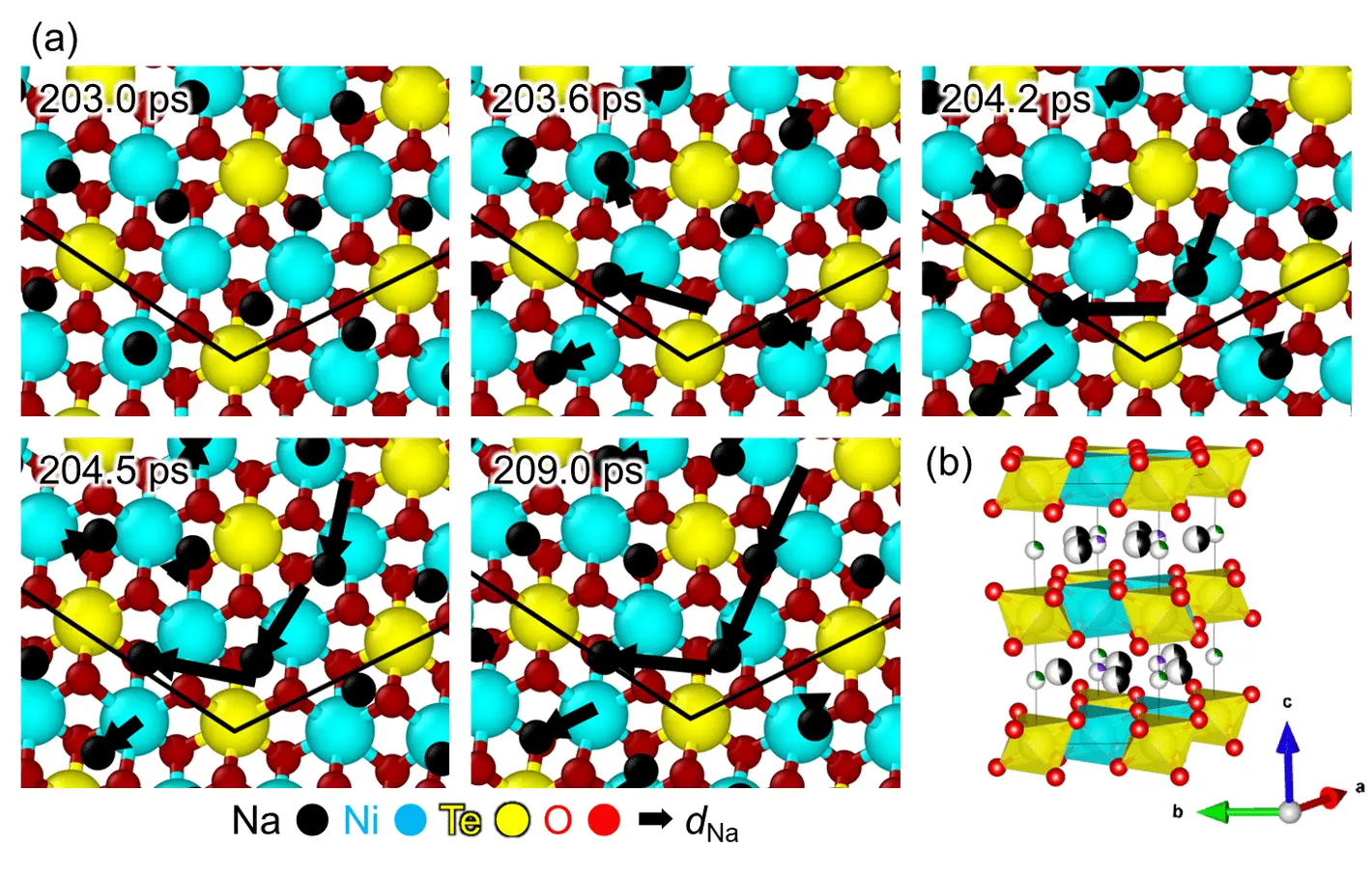
本研究で開発したモデルを用いて、さまざまな固体電解質における協奏的な輸送の様子を解析しました。図2は、層状構造をもつ二次元イオン伝導体 Na₂Ni₂TeO₆ における Na イオンの協奏的輸送を示した例です。右下の結晶構造に示すように、この材料では酸化物の多面体層の間に Na 層が挟まれており、Na イオンは主に二次元平面内を移動します。図ではこの Na 層 1 層とその直下の酸化物層のみを表示しています。t = 203 ps の位置を基準に変位ベクトルを描くと、時間とともにイオンが安定サイト間を乗り移るホッピング輸送が現れます。t = 203.6 ps では中央付近で最初のホッピングが起こり、その後の時刻では、それに続くように周囲のイオンが次々とホッピングを示し、連鎖的な協奏的輸送になっている様子がわかります。

このような短時間でのホッピングのつながりを Na 層全体でまとめたのが図3です。図に見られるように、2〜3 回のホッピングが連なった短い協奏的輸送もあれば、5〜10 個ものイオンが連動して動く長い経路も含まれていることがわかります。統計的に解析すると、5 個以上のイオンが協奏的輸送に関わる事例が全体の数十％に達しており（図3中央）、一度ホッピングが起こると、それを“引き金”として多数のイオンがなだれのように連動して動き、イオン伝導に大きく寄与していることが明らかになりました。

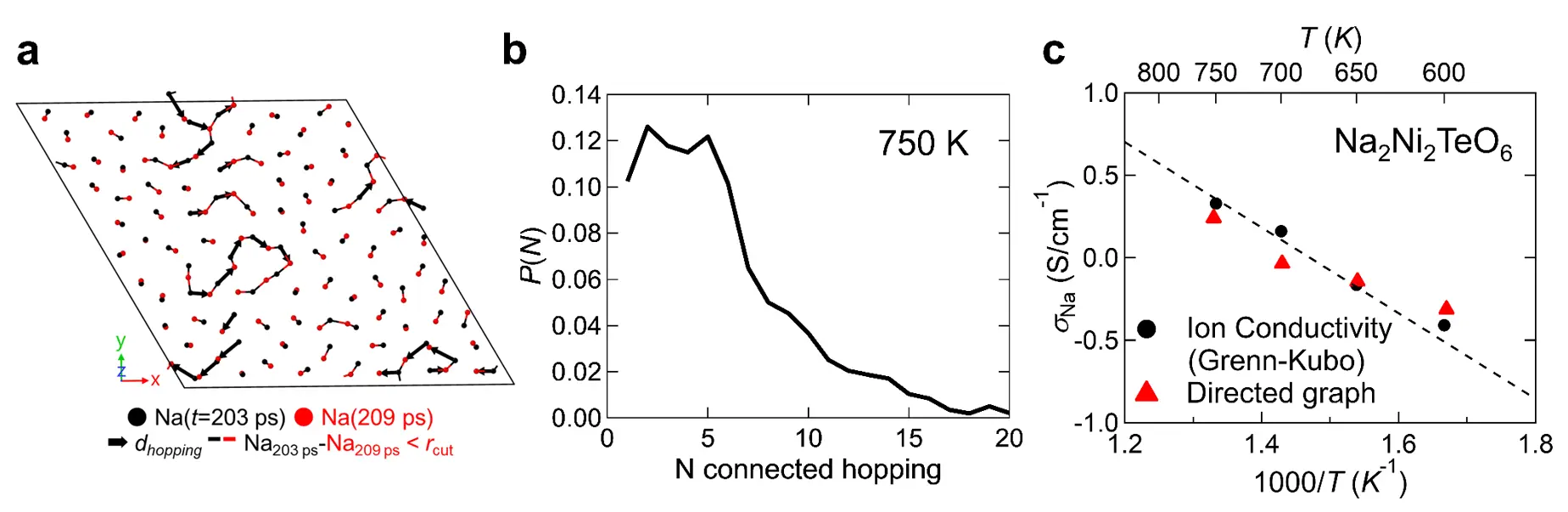
図3．（a）Na₂Ni₂TeO₆内のあるNa層のある時間区間における協奏的な輸送の軌道。（b）Na₂Ni₂TeO₆で起こった協奏的な輸送に関わったイオンの数Nの確率密度分布。（c）（a）の協奏的な輸送の軌道の「端から端までの見かけ上のイオンの移動距離」より求めたイオン伝導度（Directed graph）および実際のNa₂Ni₂TeO₆のNaイオン伝導度。

さらに、この協奏的な輸送経路の「端から端までの見かけの移動距離」を用いてイオン伝導度を計算すると、図中の赤三角で示すように、厳密な統計力学に基づく Green–Kubo公式^[用語7]の計算結果を精度よく再現できることが確認されました。すなわち、変位ベクトル（矢印）をつないで協奏的輸送を表すというシンプルな描像でありながら、実際のイオンの集団運動を正しく捉えたモデルであることが実証されました。

本研究で得られた協奏的な輸送経路を解析すると、「1つのホッピングが別のイオンのホッピングを誘発する」という因果的な連鎖が、実際のイオン伝導を大きく押し上げていることが明らかになりました。従来は、個々のイオンの自己拡散や時間方向の相関のみが主に議論されていましたが、本研究では空間的なつながりまで含めた“時空間の協奏性”を直接可視化し、それが Green–Kubo公式により定義される厳密なイオン伝導度と一致することを初めて示しました。さらに、このモデルは「あるホッピングが次のホッピングを引き起こす状況（周囲環境）」を効率よく抽出できるため、従来より議論されてきたイオン–格子相互作用などの高速イオン伝導の起源を明確化する手がかりも与えます。これらの成果は、協奏的なイオン輸送を制御して材料性能を高めるという新しい設計指針を提供するものであり、次世代固体電解質の開発への貢献が期待されます。

発表者・研究者等情報

東京科学大学総合研究院化学生命科学研究所
安藤康伸准教授

東京大学大学院工学系研究科
佐藤龍平助教
澁田靖教授

東北大学材料科学高等研究所
サウカーティック特任講師

論文情報

掲載誌：: Chemistry of Materials
タイトル：: Visualizing Concerted Ion Migration of Superionic Conductors via Directed Graphs
著者：: Ryuhei Sato*, Yasunobu Ando, Kartik Sau, Yasushi Shibuta
DOI：: 10.1021/acs.chemmater.5c02374

研究助成

本研究は、日本学術振興会（JSPS）における科学研究費助成事業学術変革領域研究（A）「イオン流の非平衡性と集団運動の理解による材料デザイン変革（JP24H02203）」、若手研究（JP23K13542、JP25K17822）および文部科学省におけるデータ創出・活用型マテリアル研究開発プロジェクト事業（DxMT）の再生可能エネルギー最大導入に向けた電気化学材料研究拠点（DX-GEM、JPMXP1122712807）の支援により実施されました。また、本研究の計算は東京大学物性研究所のスーパーコンピュータを利用し行われました。

用語説明

[用語1]: 電解質：電池が充放電する際には、負極と正極の間をリチウムイオン（Li^＋）などの荷電粒子が移動する必要がある。電解質（＝イオン伝導体）は、両極を隔てつつイオンの通り道を提供する材料であり、そのイオンの通しやすさ（輸送特性）が電池の性能や充放電速度に大きく影響する。
[用語2]: 分子動力学シミュレーション：材料を構成している原子の運動について、運動方程式を解くことによりその軌跡を追跡する計算手法。各原子に作用する力および初期位置・速度が分かれば、各時間のすべての原子の位置および速度が一意に決定される。
[用語3]: 協奏的な輸送：多数のイオンが、互いの動きに連動して効率的に移動する現象。1つのイオンが動くと、その動きに押されるように次のイオンが動き、さらにその次へ…と「玉突き」のように連鎖的な運動が続く。この集団運動が起きると、多数のイオンが一度に輸送へ貢献するうえ、移動に必要なエネルギーが低くなることも知られている。こうした協奏的輸送の仕組みを理解することは、高性能な電解質材料の設計において重要な鍵となる。
[用語4]: 有向グラフ解析：ノード（点）とノード同士を結ぶエッジ（辺）からなるネットワーク構造を扱う解析手法を「グラフ解析」と呼ぶ。有向グラフ解析では、エッジに向きが与えられ、ノードをつなぐ順序が一方向に決まっているネットワーク構造を扱う。本研究では、イオンの移動を表す変位ベクトルをノードとして扱い、ある変位ベクトルの「終点」が、別の変位ベクトルの「始点」に一定距離以内で近づいた場合にのみ、後者へ向かうエッジを結ぶ。このとき、逆方向（始点 → 他の変位の終点）にはエッジを結ばないため、ネットワークは一方向のみにつながる“有向”グラフとなる。これにより、イオンのホッピングがどのように連鎖して起こるかという因果関係を表現・解析することができる。
[用語5]: 全固体型電池：正極・電解質・負極のすべてが固体材料で構成された電池。現在広く使われているリチウムイオン電池では液体の電解質が用いられており、可燃性や液漏れなどの安全性上の問題がある。固体電解質を用いることでこれらの問題を解決できる一方、一般に液体電解質と比べてイオンの通りやすさ（輸送特性）が低いことが、全固体型電池の性能向上を妨げる主な要因となっている。
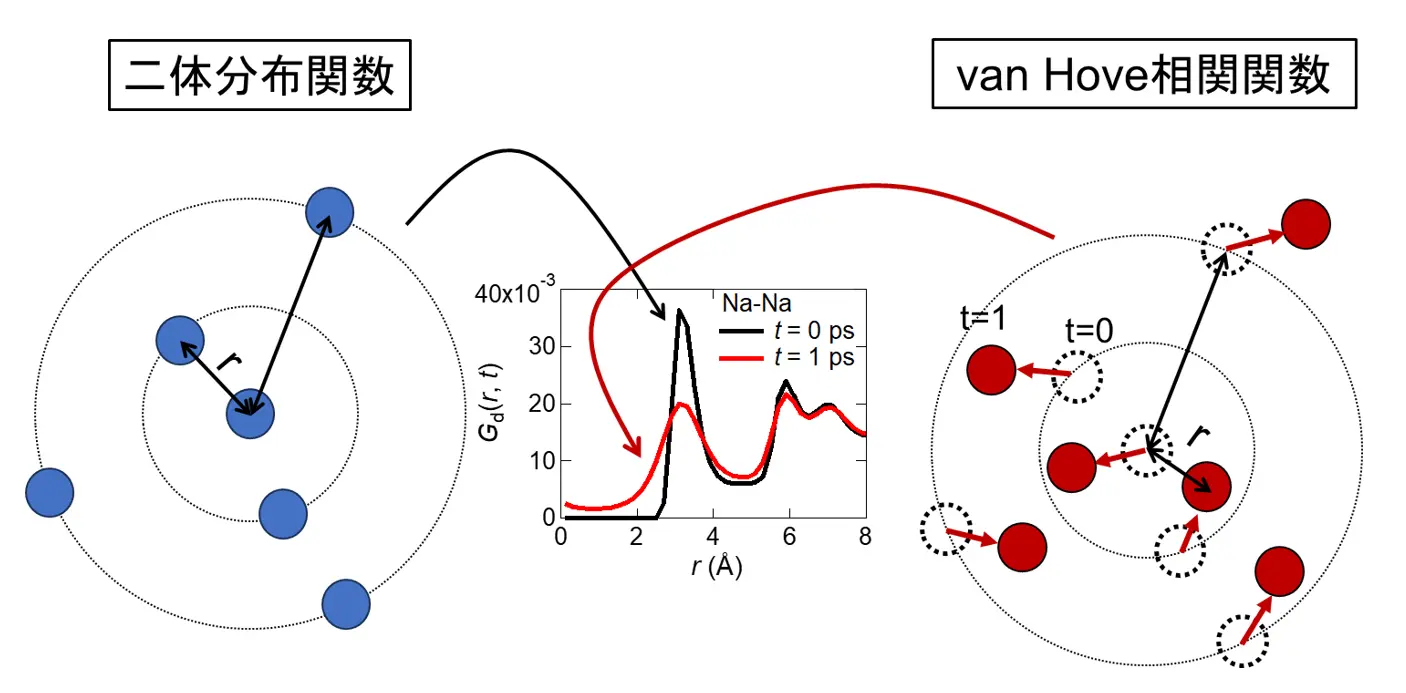
[用語6]: van Hove 相関関数：基準となるイオンのまわりに、他のイオンが“時間とともにどのように分布するか”を表す時間依存の二体相関関数。t = 0 の位置に固定した中心イオンに対して、一定時間後に周囲のイオンがどの距離に現れるかを示す。図に示すように、時間が経つにつれて中心方向へ移動してくるイオンが存在すると、van Hove 相関関数では短距離側に分布が現れる。一方、同じ時刻の瞬間的な二体分布関数にはこの短距離ピークは現れない。この違いは、中心イオンと周囲のイオンが同時に動いて互いに近づく“協奏的な運動”が起こっていることを示している。

[用語7]: Green–Kubo 公式：電気伝導度・熱伝導率・イオン伝導度などの輸送係数を、統計力学の線形応答理論から求めるための厳密な公式。イオン伝導度の場合、材料中を流れる電流の“時間相関”（電流がどれだけ長く持続するか）を分子動力学シミュレーションから計算し、その積分値として伝導度を求める。この式には、異なるイオン同士の速度の積が現れるため、イオン間の相互作用や協奏的な集団運動の効果が自然に含まれる。一方で、「何個のイオンがどのように協奏して動いたか」という因果構造までは直接読み取れない。本研究のモデルは、この因果構造を明示しつつ Green–Kuboの厳密な伝導度と一致する点が特長である。